Кроме этого предположим, система пластин в начальный момент времени прогрета равномерно и, следовательно, начальные условия для функции имеют вид (11).

При сделанных выше предположениях условия Коши (12) для этой задачи имеют вид

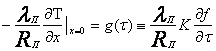(13)

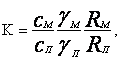Где

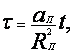
Подставляя значение из условия (2) в решение задачи Коши (3) получим

(14)

где

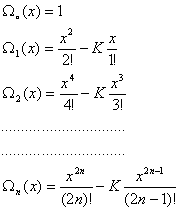
Таким образом, решение этой задачи имеет вид

(15)

где нам задана, а функции (n=1, 2, … , N) определяются из решения интегральных уравнений Вольтерра первого рода (5) методом регуляризации

(7) - (9).

Следовательно, искомые величины определяются из решения (4) с использованием регуляризирующего алгоритма (7) - (9).

Метод наименьших квадратов.

Пусть функция задана на своими значениями в точках . Рассмотрим совокупность функций

(16)

линейно независимых на .

Будем отыскивать линейную комбинацию этих функций

(17)

так, чтобы сумма квадратов ее отклонений от заданных значений функции в узлах имела бы наименьшее возможное значение, то есть величина

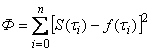(18)

принимала бы минимальное значение.

Заметим, что упомянутая сумма является функцией коэффициентов

. (19)

Страницы: 1 2 3 4 5 6 7 8 9 10